EXPONENTIAL FUNCTIONS

Definition of Exponential Function

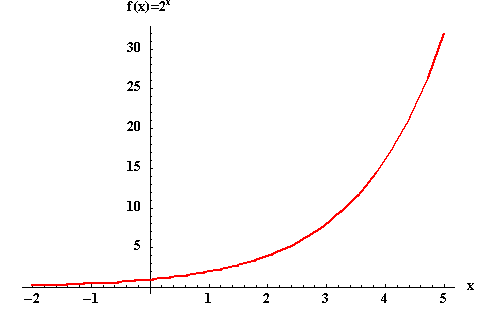
The exponential function f with base a is denoted by , where , and x is any real number. The function value will be positive because a positive base raised to any power is positive. This means that the graph of the exponential function will be located in quadrants I and II.

For example, if the base is 2 and x = 4, the function value f(4) will equal 16. A corresponding point on the graph of would be (4, 16).

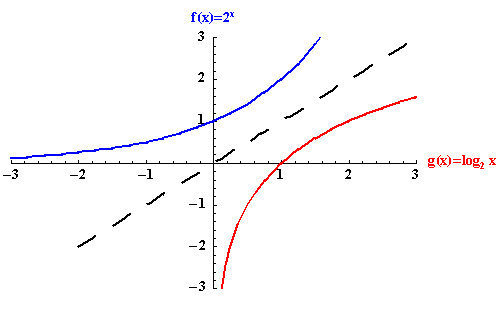
Definition of Logarithmic Function

For x >0, a>0 , and , we have

Since x > 0, the graph of the above function will be in quadrants I and IV.

Comments on Logarithmic Functions

• The exponential equation could be written in terms of a logarithmic equation as .
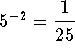• The exponential equation can be written as the logarithmic equation .
• Since logarithms are nothing more than exponents, you can use the rules of exponents with logarithms.
• Logarithmic functions are the inverse of exponential functions. For example if (4, 16) is a point on the graph of an exponential function, then (16, 4) would be the corresponding point on the graph of the inverse logarithmic function.

• The two most common logarithms are called common logarithms and natural logarithms. Common logarithms have a base of 10, and natural logarithms have a base of e.

If you are interested in reviewing any of the following topics, click the appropriate item:

• The properties of logarithms along with examples and problems, click on Properties

  • The graphs of logarithms, with examples and problems, click on Graphs of Logarithms

    • Change of base with respect to logarithms with examples and problems, click on Change of base

      • The three rules of logarithms, with examples and problems, click on Rules of Logarithms

        • Solving exponential and logarithms equations with examples and problems, click on Solving Equations

          • Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems

        

        [Exponential Rules] [Logarithms]

        [Algebra] [Trigonometry ] [Complex Variables]

        Equ MATHematics home page

      

      Author: Alexander Voznesensky
      

    Copyright © 2005-2007 EquMath.net. All rights reserved.
    Contact us