
 Knowledge of the quadratic formula is older than the Pythagorean Theorem. Solving a cubic equation, on the other hand, was the first major success story of Renaissance mathematics in Italy. The solution was first published by Girolamo Cardano (1501-1576) in his Algebra book Ars Magna.
Knowledge of the quadratic formula is older than the Pythagorean Theorem. Solving a cubic equation, on the other hand, was the first major success story of Renaissance mathematics in Italy. The solution was first published by Girolamo Cardano (1501-1576) in his Algebra book Ars Magna.
Our objective is to find a real root of the cubic equation
ax3+bx2+cx+d=0.
The other two roots (real or complex) can then be found by polynomial division and the quadratic formula. The solution proceeds in two steps. First, the cubic equation is "depressed"; then one solves the depressed cubic.
 This trick, which transforms the general cubic equation into a new cubic equation with missing x2-term is due to Nicolo Fontana Tartaglia (1500-1557). We apply the substitution
This trick, which transforms the general cubic equation into a new cubic equation with missing x2-term is due to Nicolo Fontana Tartaglia (1500-1557). We apply the substitution
to the cubic equation, to obtain:
Multiplying out and simplifying, we obtain the "depressed" cubic
Let's try this for the example
2x3-30x2+162x-350=0.
Our substitution will be x=y+5; expanding and simplifying, we obtain the depressed cubic equation
y3+6y-20=0.
We are left with solving a depressed cubic equation of the form
y3+Ay=B.
How to do this had been discovered earlier by Scipione dal Ferro (1465-1526).
We will find s and t so that
| 3st |
= |
A |
(1) |
| s3-t3 |
= |
B. |
(2) |
It turns out that y=s-t will be a solution of the depressed cubic. Let's check that: Replacing A, B and y as indicated transforms our equation into
(s-t)3+3st (s-t)=s3-t3.
This is true since we can simplify the left side by using the binomial formula to:
(s3-3s2t+3st2-t3)+(3s2t-3st2)=s3-t3.
How can we find s and t satisfying (1) and (2)? Solving the first equation for s and substituting into (2) yields:
Simplifying, this turns into the "tri-quadratic" equation
which using the substitution u=t3 becomes the quadratic equation
From this, we can find a value for u by the quadratic formula, then obtain t, afterwards s and we're done.
Let's do the computation for our example
y3+6y=20.
We need s and t to satisfy
| 3st |
= |
6 |
(3) |
| s3-t3 |
= |
20. |
(4) |
Solving for s in (3) and substituting the result into (4) yields:
which multiplied by t3 becomes
t6+20t3-8=0.
Using the quadratic formula, we obtain that
We will discard the negative root, then take the cube root to obtain t:
By Equation (4),
Our solution y for the depressed cubic equation is the difference of s and t:
The solution to our original cubic equation
2x3-30x2+162x-350=0
is given by
I will not discuss a slight problem you can encounter, if you follow the route outlined. What problem am I talking about?
Shortly after the discovery of a method to solve the cubic equation, Lodovico Ferraria (1522-1565), a student of Cardano, found a similar method to solve the quartic equation.
This section is loosely based on a chapter in the book Journey Through Genius by William Dunham.
Show that y=2 is a solution of our depressed cubic
y3+6y-20=0.
Then find the other two roots. Which of the roots equals our solution
Transform the cubic equation
x3-6x2+14x-15=0
into a depressed cubic.
Find a real root of the cubic equation in Exercise 2.
(This is for practice purposes only; to make the computations a little less messy, the root will turn out to be an integer, so one could use the Rational Zero test instead.)
 [Back] [Next: The Geometry of the Cubic Formula]
[Algebra] [Trigonometry] [Complex Variables]
[Calculus] [Differential Equations] [Matrix Algebra]
[Back] [Next: The Geometry of the Cubic Formula]
[Algebra] [Trigonometry] [Complex Variables]
[Calculus] [Differential Equations] [Matrix Algebra]
 EquMATHematics home page
EquMATHematics home page
 A. Voznesesnky
A. Voznesesnky
98-05-20
Copyright © 2005-2007 EquMath.net. All rights reserved.
Contact us

 Knowledge of the quadratic formula is older than the Pythagorean Theorem. Solving a cubic equation, on the other hand, was the first major success story of Renaissance mathematics in Italy. The solution was first published by Girolamo Cardano (1501-1576) in his Algebra book Ars Magna.
Knowledge of the quadratic formula is older than the Pythagorean Theorem. Solving a cubic equation, on the other hand, was the first major success story of Renaissance mathematics in Italy. The solution was first published by Girolamo Cardano (1501-1576) in his Algebra book Ars Magna.
 This trick, which transforms the general cubic equation into a new cubic equation with missing x2-term is due to Nicolo Fontana Tartaglia (1500-1557). We apply the substitution
This trick, which transforms the general cubic equation into a new cubic equation with missing x2-term is due to Nicolo Fontana Tartaglia (1500-1557). We apply the substitution
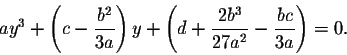
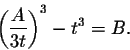

 EquMATHematics home page
EquMATHematics home page
